책 이야기

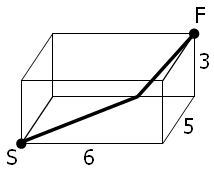
A spider, S, sits in one corner of a cuboid room, measuring 6 by 5 by 3, and a fly, F, sits in the opposite corner. By travelling on the surfaces of the room the shortest "straight line" distance from S to F is 10 and the path is shown on the diagram.

However, there are up to three "shortest" path candidates for any given cuboid and the shortest route doesn't always have integer length.

It can be shown that there are exactly 2060 distinct cuboids, ignoring rotations, with integer dimensions, up to a maximum size of M by M by M, for which the shortest route has integer length when M = 100. This is the least value of M for which the number of solutions first exceeds two thousand; the number of solutions when M = 99 is 1975.

Find the least value of M such that the number of solutions first exceeds one million.

S라는 거미가 가로 6, 세로 5, 높이 3인 육면체 방의 구석에 있고, 반대쪽 코너에는 파리 F가 있다. 방 표면을 따라 S에서 F로 가는 가장 짧은 "직선" 거리는 10이고, 경로는 다음 그림과 같다.

그러나, 육면체 방에서는 3개의 최단 경로 후보가 있으며, 최단 경로는 정수길이가 아닐 수 있다.

회전을 무시하고, M=100일때 최대 가로 M(이하), 세로 M(이하), 높이 M(이하)이고 최단 경로가 정수인 육면체는 2060개가 있다. 이것은 M이 99일 때, 최단 경로가 정수인 육면체는 1975개 이며, 100일 때 처음으로 육면체의 수가 2천을 넘는다.

최단 경로가 정수인 육면체의 숫자가 1백만을 넘는 첫 M을 구하시오.

--------------------------------------------------------------------------

문제에서 회전을 무시한다고 했으므로, 경우의 수를 줄여서 계산해야 한다.

육면체에서 면의 길이 순서대로 a, b, c라고 한다면, 1<=a<=b<=c<=M이 된다. 이 조건에서, c**2+(a+b)**2의 제곱근이 자연수인 경우를 찾으면 된다.

a, b, c에 대한 3번의 반복문이 있어 실행시간이 필요하지만, 반복문을 구성할 때 위 조건에 따라 잘 정리한다면(b는 a값부터 반복문을 시작하고, a, b의 최대값은 c) 그렇게 어렵지 않게 구현 가능하다.

By counting carefully it can be seen that a rectangular grid measuring 3 by 2 contains eighteen rectangles:

Although there exists no rectangular grid that contains exactly two million rectangles, find the area of the grid with the nearest solution.

3x2 그리드에서 볼 수 있는 사각형을 주의깊게 세어 보면 18개가 나온다:

정확하게 2백만 개 사각형이 있는 그리드는 없지만, 2백만에 가장 가까운 그리드를 구하시오.

--------------------------------------------------------------------------

가로 세로로 나눠 생각해보면, 크기 3인 면(3x1 그리드)에 크기 1의 사각형은 3개, 크기 2의 사각형은 2개, 크기 3의 사각형은 1개 들어간다. 즉, (크기-사각형 크기+1)의 합계가 된다. 여기에 세로 길이를 고려하여 갯수를 구하면(가로x세로) 전체 사각형 갯수가 나온다.

이 문제에서는 2백만에 가장 가까운 그리드를 요구했는데, 2백만 보다 큰 지 작은 지 정확히 나오지 않아 두 경우를 모두 고려해야 했다.

그리고, 가로, 세로 크기에 한계를 정하지 않은 상태여서 그 부분을 미리 유추해야 할 필요가 있다. 가만히 보면 가로 합계x세로 합계가 형태이므로, (x(x+1)/2)*(y(y+1)/2)의 공식이 나오게 된다. 즉, x²*y²이므로 가로 세로가 100일 때 천만 이상의 사각형이 나오게 되므로, 여유를 주고 반복문을 통해 2백만에 근접한 값을 구하게 했다.

공식을 생각하기 전에 사각형 갯수를 구하는 반복문을 만들어서 그대로 썼는데, 간단한 공식으로 구할 것을 사각형 크기별로 합계를 모두 구하게 해서, 실행 속도를 손해보게 된 것 같다.

NOTE: This problem is a more challenging version of Problem 81.

The minimal path sum in the 5 by 5 matrix below, by starting in any cell in the left column and finishing in any cell in the right column, and only moving up, down, and right, is indicated in red and bold; the sum is equal to 994.

Find the minimal path sum from the left column to the right column in matrix.txt (right click and "Save Link/Target As..."), a 31K text file containing an 80 by 80 matrix.

주의: 이 문제는 문제81 보다 더 어렵다.

첫번째 열의 원소에서 시작해서 마지막 열에서 끝나며 위, 아래, 오른쪽으로만 움직일 때 아래의 5x5 행렬에서 최소 경로는 붉은 색으로 굵게 표시되어 있으며 합계는 994이다.

80x80 행렬이 있는 31K 텍스트 파일 matrix.txt (우클릭 하고 "다른 이름으로 링크 저장")의 첫번째 열에서 마지막 열까지 이동할 때 최소 경로의 합계를 구하시오.

--------------------------------------------------------------------------

81번 문제를 해결한 방법을 그대로 사용할 수는 없었지만, 그 방법을 가져와서 반복을 통해 해결했다. 81번 문제에서는 답을 구할 자리가 행렬 전체의 마지막 자리(80, 80)이지만, 이번 문제에서는 마지막 열(x,80) 모두가 답이 되는 후보이기 때문에 마지막 열 각 행을 기준으로 최소 경로의 값을 구하는 방식으로 접근했다..

위 예시를 기준으로 예를 들면, 2번째 열, 2번째 행의 최소값 후보는 1번째 열 각 행에서 시작한 5개 경로의 값 900(131+673+96), 297(201+96), 1529(630+803+96), 2135(537+699+83+96), 3135(805+732+699+803+96) 중 가장 작은 297이 된다. 이 예시에서 131다음에 201로는 왜 안가고 673으로만 가는지 의문이 들 수 있는데, 이 경우 201에서 시작한 경우보다는 무조건 크기 때문에 최소값이 될 수 없다고 생각해서 배제했다.

이런 식으로 각 열의 최소값을 2번째 열부터 마지막 열까지 구하고, 마지막 열 각 행의 최소 경로 값 중에서 제일 작은 값을 찾으면 된다. 그런데, 다중 반복문을 실행하느라 시간이 7초 이상 걸리는 것을 보면 좀 더 빠른 방식으로 해결하는 방법이 있을 것 같다.

In the 5 by 5 matrix below, the minimal path sum from the top left to the bottom right, by only moving to the right and down, is indicated in bold red and is equal to 2427.

Find the minimal path sum from the top left to the bottom right by only moving right and down in matrix.txt (right click and "Save Link/Target As..."), a 31K text file containing an 80 by 80 matrix.

아래의 5x5 행렬에서, 오른쪽과 아래로만 갈 수 있을 때 왼쪽 위부터 오른쪽 아래까지 가는 최소 경로값은 굵은 붉은색으로 표시된 것과 같으며 2427이다.

80x80 행렬이 있는 31K 텍스트 파일 matrix.txt (우클릭하고 "다른 이름으로 링크 저장")을 오른쪽과 아래로만 갈 수 있을 때 , 왼쪽 위부터 오른쪽 아래까지 가는 최소경로 합계를 구하시오.

--------------------------------------------------------------------------

파일을 다루는 것에 익숙하지 않아서 파일을 열고, 내용을 읽고, 쉼표로 분리하고, 문자열을 숫자로 바꾸는 과정 하나하나를 다시 기억을 살려가며 해야 했다.

처음에는 단순하게 갈 수 있는 두 경우 중 작은 경우로 가는 것을 0,0과 79,79에서 시작하도록 해봤는데 오답이었다.

그래서, 생각해보니 방향이 제한적이기 때문에 조금은 단순하게 접근 가능할 것 같았다. 0,0부터 시작해서 차례로 이전과의 합계를 기록해 나가는 방식으로 하면, 79,79에 전체 합계가 기록되는 것이다. 각 자리에서는 자신에게 올 수 있는 2가지 경우의 합계 중 작은 것을 선택해 나가는 방식으로 하는 것이다.

이후 문제에까지 확장하여 적용하는 것은 쉽지 않을 것 같았는데, 일단 이 문제는 이 방식으로 해결 가능했다.

It is well known that if the square root of a natural number is not an integer, then it is irrational. The decimal expansion of such square roots is infinite without any repeating pattern at all.

The square root of two is 1.41421356237309504880⋯, and the digital sum of the first one hundred decimal digits is 475.

For the first one hundred natural numbers, find the total of the digital sums of the first one hundred decimal digits for all the irrational square roots.

자연수의 제곱근이 정수가 아니면, 무리수가 된다. 이러한 제곱근의 소숫점은 반복되지 않으면서 무한하게 확장된다.

2의 제곱근은 1.41421356237309504880⋯이며, 소숫점 처음 100자리 숫자의 합은 475이다. 

100까지 자연수 중에서 제곱근이 무리수인 숫자의 소숫점 처음 100자리 숫자의 총합은 얼마인가?

--------------------------------------------------------------------------

처음에는 연분수 문제(문제 64)를 응용해서 간단하게 해결하려 했는데, 제곱근을 직접 계산하지 않으면 소숫점 이하에서 오차가 발생하는 문제가 있어, 제곱근을 손으로 계산하는 방법을 찾아 알고리즘으로 구현했다.

위 링크의 방법2에 왠만한 설명보다 자세하게 나와있기 때문에 코딩하는 데 그리 어렵지 않을 것이다. 프로그램으로 만드는 과정에서 break를 뺀다든지 하는 몇가지 오류가 있어 수정하는 데 시간은 좀 걸렸지만 재미있게 해결 가능한 문제였다.