책 이야기

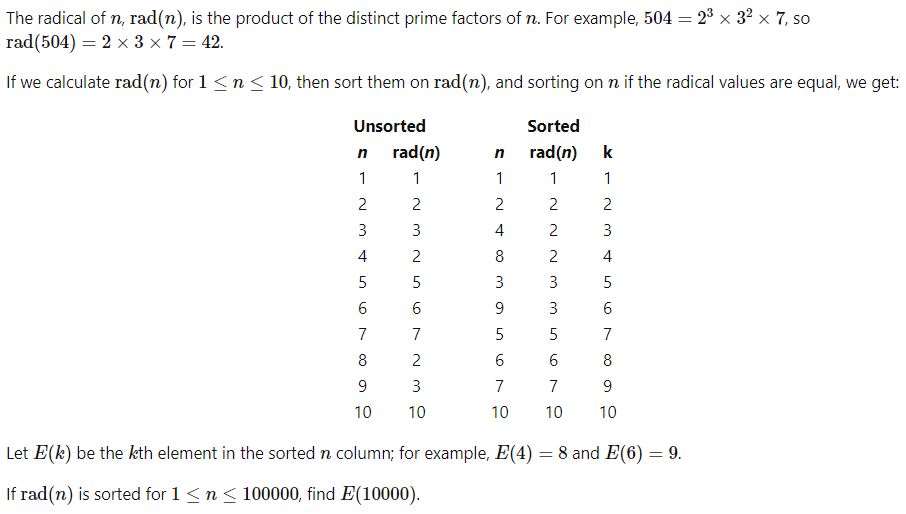
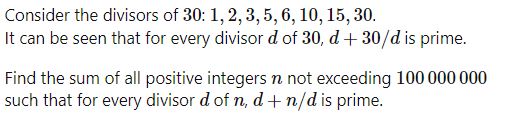양의 정수 a,b,c,d가 ab=cd=N이고 a+b=c+d+1인 경우, 양의 정수 N은 은밀하다고(stealthy) 한다.

예를 들어, 36=4x9=6x6은 은밀하다.

10⁶ 이하에는 2851개의 은밀한 숫자(Stealthy Numbers)가 있다.

10¹⁴ 이하에는 몇 개의 은밀한 숫자가 있는가?

--------------------------------------------------------------------------

문제는 그리 까다롭지 않아, 문제에서 요구한 것만 구현하면 코드가 그리 길지 않다. 숫자의 약수를 구해서, 약수가 n개인 경우 n/2개까지 두 숫자를 각각 a, c로 두고, b, d를 연산을 통해 구하고, a+b=c+d+1인 경우를 찾도록 만들었다.

하지만, 예시로 나온 1백만 이하에 몇 개가 있는지 검증하는데 벌써 속도 문제를 만나게 되었다. 문제에서 요구한대로 했을때 구해지는 답을 보고 4의 배수만 나오기 때문에 그것으로 성능을 조금 개선했다. 그래도, 약수를 구하는 부분에서 시간이 많이 소요되어서, 대상 숫자를 보니 전체 약수의 가운데 부근에 있었다. 예를 들어 설명하면 약수가 10개인 경우 4,5번째 숫자 또는 3,4번째 숫자가 a,c가 되는 것이었다. 그렇게 해서 속도를 개선하니 1백만 개 이하의 은밀한 숫자 갯수를 맞게 구할 수 있어서 문제에서 요구한 대로 구현했음을 알 수 있었다.

하지만, 1백만 개에 9초의 시간이 필요했으면, 문제에서 요구한 1경 개를 대상으로 구하려면 적어도 900000000초(250000시간)의 시간이 필요한 상황임을 알 수 있었다. 그 말은 문제를 있는 대로 구현하는 것이 아니고 새로운 알고리즘을 찾는 것을 요구하는 정수론 문제라는 것이었다.

인터넷을 검색해 보니, 깃헙에 누군가가 구현한 내용에서 bipronics라는 명칭으로 x*(x+1)*y*(y+1)을 구하는 정수 배열을 활용해서 구했다고 설명했는데, 그 정수 배열이 문제에서 요구하는 답과 동일한 것이었다. 왜 약수 중에 a+b=c+d+1인 약수와 x*(x+1)*y*(y+1)이 동일한지 이해는 안되었지만 그렇다고 한다. 처음 접근한 방법으로 안되었을 때, 숫자 리스트를 만들고 a+b=c+d+1을 만족하는 경우에 flag을 바꾸는 형태로 해결할 수 있을지 고민하다가, 변수가 너무 많아 포기했는데 조금은 비슷한 접근인 것 같기도 했다.

이 개념으로 구현하니 1백만 개는 0.04초만에 구할 수 있었는데, 그래도 1경 개를 구하는 데에는 시간이 꽤나 걸렸다. 조건에 맞는 리스트를 구하는 것보다 중복을 제거하는 데 시간이 더 많이 걸린 것이 함정이었다. 파이썬의 list(set())의 조합으로 중복을 제거했는데, 7천만 개 이상 리스트에서 중복 제거하는 데 많은 시간을 필요로 했다. 대충 1분 이내에 조건에 맞는 리스트를 구했는데 거기에서 중복을 제거하는 데 10분 이상 소요되었다.

30의 약수는 1, 2, 3, 5, 6, 10, 15, 30이다.

30의 모든 약수인 d와 d+30/d는 소수이다.

100000000이하의 정수 n의 약수 d가 있을 때, 모든 d+n/d가 소수인 n의 합계를 구하시오.

--------------------------------------------------------------------------

처음에는 정직하게 접근해서 1에서 1억 사이의 숫자를 대상으로 약수(d)를 구하고 d+n/d가 소수인 숫자를 찾게 했다. 시간이 많이 걸려서 생각해 보니 d+n/d가 소수이려면, d=n일 경우 n+1이 소수이고 2를 제외하고 모든 소수는 홀수이므로 n은 짝수여야 한다. 그리고 짝수의 경우 d=2일 때 n/2가 홀수여야 하므로 4의 배수가 되면 안된다. 그러므로, 2, 6, 10으로 커지는 4i+2의 경우만 검증하면 된다. 이렇게 해서 실행시간을 많이 줄였지만 1억까지 계산하려면 여전히 많은 시간을 필요로 했다.

그래서, 접근을 바꿔서 1000이하의 숫자(d)의 반복문과, d부터 시작해서 n/d를 구하는 이중 반복문을 만들고, 두 수의 합계가 소수가 아닌 경우에는 원 숫자에 표시하도록 처리해서, 남는 수의 합을 구하도록 해결책을 다르게 접근해서 9분 이내에 답을 구할 수 있었다. 

참고로, 챗gpt의 성능 테스트겸 357번 문제를 물어봤는데 문제에서 요구하는 그대로 가장 정직하게 프로그램을 제시했다. 성능 문제만 고려하지 않으면 즉시 적용 가능하도록 구현해 내는 것이 어찌보면 대단하다 싶었다.

양의 정수 x, y, z가 등차수열의 연속된 요소일 때, x2-y2-z2=n으로 구해지는 가장 작은 양의 정수 n은 n=27일 때 정확하게 2개의 해답이 있다:

342-272-202=122-92-62=27.

정확하게 10개의 해답이 있는 최소값은 n=1155일 때이다.

10개의 해답이 있는 1백만 이하의 n은 몇 개 인가?

--------------------------------------------------------------------------

등차수열이기 때문에 처음에는 x를 기준으로, x2-(x-a)2-(x-2a)2=n으로 수식을 만들어서, 정리하니 x2-6ax+5a2=-n이어서, (x-a)(x-6a)=-n이 되었다. 모양은 좀 이상했지만 처음 값 x와, 차이 a 기준으로 n의 약수의 곱이 된다는 것을 알 수 있었다.

(제대로 접근한 사람은 가운데 y를 기준으로 (y+a)2-y2-(y-a)2=n으로 수식을 만들어서, 전개하면 4ay-y2=n이 되고, 차이 a 기준으로 정리하면 a=(n+y2)/4y가 된다)

처음에는 약수의 갯수만 관련이 있다고 생각하고 약수가 20개 인 수(두 수의 곱이므로 절반인 10개의 해답을 만드는 수로 추정)의 갯수를 찾도록 구현했는데, 약수 만드는 함수의 성능이 나빠서 시간이 너무 많이 걸리고, 이를 개선해서 조금 빨리 돌아가도록 했는데 오답이 나왔다.

다시 확인해보니, 후보가 되는 것은 약수가 맞지만 두 약수의 곱이 아니기 때문에 약수를 대상으로 등차수열 조건(a=(n+y2)/4y, a<y, a는 정수)을 만족하는지 확인해야 되는 것이었다. 그렇게, 단순히 약수의 갯수를 세는 것이 아니라 약수를 대상으로 등차수열을 만들 수 있는 것이 몇 개인지 확인하도록 변경해서 답을 구할 수 있었다.

그리고, 처음에는 n의 약수를 1~n/2까지 비교하도록 되어 있던 함수 성능을 개선한 이후에야 수분 내에 답을 구할 수 있어서, 성능의 중요성을 다시 한 번 느꼈다.

n의 근인 rad(n)은 서로 다른 소수 n의 곱이다. 예를 들어, 504=2³*3²*7이고, rad(504)=2*3*7=42이다.

n이 1이상, 10이하일 때 rad(n)을 계산하고, rad(n)을 기준으로 정렬하고, 근 값이 같을 때 n 값에 따라 정렬하면 위의 표와 같다:

E(k)를 정렬된 n의 k번째 요소라고 하자. 예를 들어, E(4)=8이고, E(6)=9이다.

rad(n)이 1이상, 10만 이하의 값으로 정렬되었을 때, E(10000)을 구하시오.

--------------------------------------------------------------------------

미리 만들어 둔 약수 함수를 이용해서 결과 중 소수만 찾으면 rad(n) 값을 구할 수 있다.

10만개 결과 리스트에 대해 rad(n)값을 1순위, n값을 2순위로 해서 정렬하면 답을 구할 수 있다. 파이썬 리스트의 인덱스가 0부터 시작하는 것 때문에 1만번째 값을 다른 것을 구하는 덕분에 다시 한 번 더 실행해야 되어서 시간이 좀 걸렸다.

약수 함수를 아무리 개선해도 성능에 한계가 있어서 문제에서 10만개를 요구했으니 다행이지 다른 문제처럼 몇조 단위의 처리를 요구했으면 시간내에 해결하지 못했을 것 같다.

다음 수식에서 x, y, n은 양의 정수이다.

1/x+1/y=1/n

n이 4일 때, 다음의 3개 답안만 있다:

1/5+1/20=1/4

1/6+1/12=1/4

1/8+1/8=1/4

서로 다른 해결책이 1,000개를 넘는 가장 작은 값 n은 얼마인가?

주의: 이 문제는 문제 110의 쉬운 버전이므로, 이 문제를 먼저 해결하기를 강력하게 권고함

--------------------------------------------------------------------------

다른 분이 이야기한 아이디어(양변에 nxy를 곱해서 분모 없애기)를 참고해서 해결할 수 있었다.

문제에 나오는 공식의 분모를 없애기 위해 간단히 수학을 적용해서 양변에 xyn을 곱하면 ny+nx=xy가 된다. 그리고, 예시를 보면 짐작 가능하겠지만 n이 x, y보다는 작기 때문에 x를 n+a, y를 n+b로 바꾸면 n(n+b)+n(n+a)=(n+a)(n+b)가 된다. 이를 풀면 n²+nb+n²+na=n²+na+nb+ab가 되고 양변을 정리하면 n²=ab가 된다.

이 특성을 이해하고, 예시를 다시 보면 x의 값이 n=4일 때, n보다 1, 2, 4만큼 큰 것을 알 수 있다. 이것이 4의 약수이기 때문에, 솔루션이 1000개를 넘는 것은 약수가 1000개를 넘는 경우와 같은 것으로 이해되었다. 그래서, 먼저 풀었던 243번 문제에서 적용한 소수의 곱을 대상으로 배수로 키워나가면서 약수가 1000개 이상인 경우를 찾는 방법을 적용했는데, 예상과는 달리 오답이었다.

n²=ab를 다시 생각해보니, n의 약수가 아니라 n²의 약수 중 n이하의 값인 것들을 찾으면 되는 것이었다. 예시로 나온 4가 너무 작은 수이면서 2의 배수여서 다양한 경우가 나오지 않아 잘못된 유추를 하게 되었던 것이다.

약수를 구하는 함수를 n제곱을 입력값으로 해서 n이하의 값만 구하도록 바꾸고 나니 빠른 시간 내에 답을 구할 수 있었다.

The sequence of triangle numbers is generated by adding the natural numbers. So the 7th triangle number would be 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28. The first ten terms would be:

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...

Let us list the factors of the first seven triangle numbers:

 1: 1

 3: 1,3

 6: 1,2,3,6

10: 1,2,5,10

15: 1,3,5,15

21: 1,3,7,21

28: 1,2,4,7,14,28

We can see that 28 is the first triangle number to have over five divisors.

What is the value of the first triangle number to have over five hundred divisors?

삼각수 수열은 자연수를 더하면서 생성된다. 따라서, 7번째 삼각수는 1+2+3+4+5+6+7=28이다. 처음 10개 요소는 다음과 같다.

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...

처음 일곱 개 삼각수의 인수를 나열해 보면,

 1: 1

 3: 1,3

 6: 1,2,3,6

10: 1,2,5,10

15: 1,3,5,15

21: 1,3,7,21
28: 1,2,4,7,14,28

28은 처음으로 5개가 넘는 약수를 가지는 수임을 알 수 있다. 500개 약수를 가지는 첫 삼각수는 무엇인가?

--------------------------------------------------------------------------

삼각수라는 단어가 익숙하지 않았는데, 1부터 시작하는 연속된 자연수의 합을 뜻한다고 한다. 인수를 구하는 함수를 작성하고, 반복문을 통해 인수가 처음으로 500개 이상인 삼각수를 구하면 된다.

좀 더 효율적으로 구하려면, 소수인 인수의 곱으로 나타내고, 제곱수를 이용하면 된다. 5번 문제와 연관있는 부분이기도 한데, 예를 들어 28은 2²x7¹이므로 제곱수는 각각 2, 1이며, 약수의 갯수는 (2+1)(1+1)=6이 되는 특성을 활용하여 답을 구할수도 있을 것이다.