In the game, Monopoly, the standard board is set up in the following way:
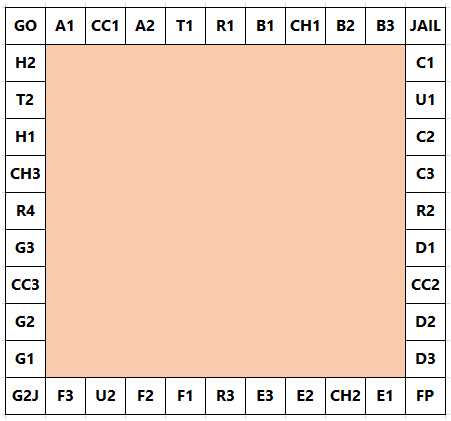
A player starts on the GO square and adds the scores on two 6-sided dice to determine the number of squares they advance in a clockwise direction. Without any further rules we would expect to visit each square with equal probability: 2.5%. However, landing on G2J (Go To Jail), CC (community chest), and CH (chance) changes this distribution.
In addition to G2J, and one card from each of CC and CH, that orders the player to go directly to jail, if a player rolls three consecutive doubles, they do not advance the result of their 3rd roll. Instead they proceed directly to jail.
At the beginning of the game, the CC and CH cards are shuffled. When a player lands on CC or CH they take a card from the top of the respective pile and, after following the instructions, it is returned to the bottom of the pile. There are sixteen cards in each pile, but for the purpose of this problem we are only concerned with cards that order a movement; any instruction not concerned with movement will be ignored and the player will remain on the CC/CH square.
- Community Chest (2/16 cards):
- Advance to GO
- Go to JAIL
- Chance (10/16 cards):
- Advance to GO
- Go to JAIL
- Go to C1
- Go to E3
- Go to H2
- Go to R1
- Go to next R (railway company)
- Go to next R
- Go to next U (utility company)
- Go back 3 squares.
The heart of this problem concerns the likelihood of visiting a particular square. That is, the probability of finishing at that square after a roll. For this reason it should be clear that, with the exception of G2J for which the probability of finishing on it is zero, the CH squares will have the lowest probabilities, as 5/8 request a movement to another square, and it is the final square that the player finishes at on each roll that we are interested in. We shall make no distinction between "Just Visiting" and being sent to JAIL, and we shall also ignore the rule about requiring a double to "get out of jail", assuming that they pay to get out on their next turn.
By starting at GO and numbering the squares sequentially from 00 to 39 we can concatenate these two-digit numbers to produce strings that correspond with sets of squares.
Statistically it can be shown that the three most popular squares, in order, are JAIL (6.24%) = Square 10, E3 (3.18%) = Square 24, and GO (3.09%) = Square 00. So these three most popular squares can be listed with the six-digit modal string: 102400.
If, instead of using two 6-sided dice, two 4-sided dice are used, find the six-digit modal string.
표준 보드 게임인 '모노폴리'는 위 그림과 같이 구성된다.
플레이어는 GO에서 시작하고, 육면체 주사위 2개를 굴려 나온 값만큼 시계방향으로 진행한다. 추가 규칙이 없으면 각 자리를 방문할 확률은 2.5%로 동일하다. 그러나, G2J(감옥으로 가시오), CC(보물상자), CH(기회)를 방문하면 확률은 바뀐다.
G2J를 방문하거나, CC, CH에 있는 한 장의 카드를 뽑으면 플레이어는 감옥으로 가야한다. 플레이어가 같은 숫자를 3번 연속으로 굴리지 못하면, 3번째 굴린 결과까지는 진행하지 못하고, 감옥으로 곧장 가게 된다.
게임을 시작할 때, CC, CH카드는 섞어 둔다. 플레이어가 CC, CH에 도착하면 각 파일 가장 위에 있는 카드를 뽑아, 지시사항을 따르고, 뽑은 카드는 가장 파일 가장 아래에 둔다. 각 파일에는 16개 카드가 있지만, 이번 문제의 목적을 위해 이동을 명령하는 카드만 고려하고, 이동과 관련없는 카드는 무시되고 플레이어는 CC/CH 자리에 남아있게 된다.
- 보물 상자 (2/16 카드):
- GO로 이동하시오
- 감옥(JAIL)으로 가시오
- 기회 (10/16 카드):
- GO로 이동하시오
- 감옥(JAIL)으로 가시오
- C1로 가시오
- E3으로 가시오
- H2로 가시오
- R1로 가시오
- 다음 R(열차 회사)로 가시오
- 다음 R로 가시오
- 다음 U(전력(utility) 회사)로 가시오
- 3칸 뒤로 가시오
이번 문제의 핵심은 특정 자리를 방문하게 될 것을 고려하는 것이다. 즉, 주사위를 굴린 후 특정 자리를 끝낼 확률을 말한다. 이런 이유로 끝낼 확률이 0인 G2J를 제외하고, CH는 5/8이 다른 자리로 이동하게 하므로 가장 낮은 확률을 가지고, 플레이어가 각 롤을 끝낼 때 우리가 관삼가지는 마지막 자리이다. 우리는 감옥의 단순 방문과 감옥으로 보내는 것에 차이를 두지 않을 것이고, 다음 순서에 나오기 위해 지불할 것이라 가정하고 "감옥에서 나오기 위한" 같은 숫자를 요구하는 규칙 또한 무시할 것이다.
GO에서 시작해서 각 자리에 번호를 00에서 39까지 매기면, 대응하는 자리 집합을 2자리 문자열을 결합하여 만들수 있다.
통계적으로, 가장 인기 있는 자리 3개를 순서대로 보면, 10번 자리인 감옥(6.24%), 24번 자리인 E3(3.18%), 0번 자리인 GO(3.09%)이다. 이 셋은 가장 인기있는 자리이고 6자리 숫자로 표현하면 102400이다.
육면체 대신 사면체 주사위를 굴릴 경우 (가장 인기있는 3자리를 결합한) 6자리 숫자를 구하시오.
--------------------------------------------------------------------------
부루마불이라 부르는 모노폴리를 단순화하여 문제를 만든 것인데, 문제에서 요구한 조건을 정리하면 다음과 같다.
주사위 결과에 따라 이동하는데, 같은 숫자가 3번 나오면 감옥으로 이동, 보물상자(CC)와 기회(CH)에서는 뽑은 카드 결과에 따라 이동, G2J에 가면 감옥으로 이동한다. 그 외 모노폴리에 있는 부동산 구매 등은 생략하고 이동 중심으로만 했으며, 감옥을 빠져나오는 조건도 따로 두지 않았다.
가장 많이 방문하는 3곳을 구하라는 것인데, 어떻게 할 것인지 고민하다가 주사위 2개를 랜덤하게 굴리는 형태로 많은 횟수를 실제 게임을 해서 방문하는 장소를 카운트하는 형태로 구하기로 했다. 나중에 찾아보니 이것을 몬테 카를로 방법이라 부른다고 한다.
여기까지 정리되고 나니 구현하는 것은 그렇게 어렵지 않았다. 다만, 기본값 설정 등에 있어 명확하게 하지 않은 부분에서 잘못 동작되어 처음에는 오답이 나왔었다.