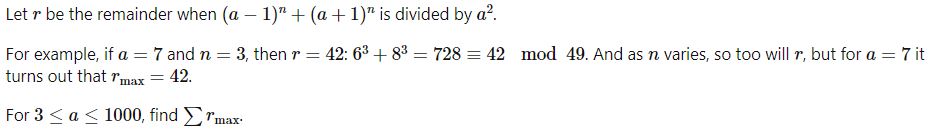책 이야기

다음 수식에서 x, y, n은 양의 정수이다.

1/x+1/y=1/n

n이 4일 때, 다음의 3개 답안만 있다:

1/5+1/20=1/4

1/6+1/12=1/4

1/8+1/8=1/4

서로 다른 해결책이 1,000개를 넘는 가장 작은 값 n은 얼마인가?

주의: 이 문제는 문제 110의 쉬운 버전이므로, 이 문제를 먼저 해결하기를 강력하게 권고함

--------------------------------------------------------------------------

다른 분이 이야기한 아이디어(양변에 nxy를 곱해서 분모 없애기)를 참고해서 해결할 수 있었다.

문제에 나오는 공식의 분모를 없애기 위해 간단히 수학을 적용해서 양변에 xyn을 곱하면 ny+nx=xy가 된다. 그리고, 예시를 보면 짐작 가능하겠지만 n이 x, y보다는 작기 때문에 x를 n+a, y를 n+b로 바꾸면 n(n+b)+n(n+a)=(n+a)(n+b)가 된다. 이를 풀면 n²+nb+n²+na=n²+na+nb+ab가 되고 양변을 정리하면 n²=ab가 된다.

이 특성을 이해하고, 예시를 다시 보면 x의 값이 n=4일 때, n보다 1, 2, 4만큼 큰 것을 알 수 있다. 이것이 4의 약수이기 때문에, 솔루션이 1000개를 넘는 것은 약수가 1000개를 넘는 경우와 같은 것으로 이해되었다. 그래서, 먼저 풀었던 243번 문제에서 적용한 소수의 곱을 대상으로 배수로 키워나가면서 약수가 1000개 이상인 경우를 찾는 방법을 적용했는데, 예상과는 달리 오답이었다.

n²=ab를 다시 생각해보니, n의 약수가 아니라 n²의 약수 중 n이하의 값인 것들을 찾으면 되는 것이었다. 예시로 나온 4가 너무 작은 수이면서 2의 배수여서 다양한 경우가 나오지 않아 잘못된 유추를 하게 되었던 것이다.

약수를 구하는 함수를 n제곱을 입력값으로 해서 n이하의 값만 구하도록 바꾸고 나니 빠른 시간 내에 답을 구할 수 있었다.

r을 (a-1)ⁿ+(a+1)ⁿ을 a²으로 나누었을 때 나머지로 하자.

예를 들어, a=7이고 n=3일 때, r=42가 된다(6³+8³=728≡42 mod 49). 그리고 n 값이 바뀌면 r도 바뀌게 된다. 하지만, a=7일 때 r의 최대값인 r_max=42이다.

3≤a≤1000일 때, r_max의 합계(∑r_max)를 구하시오.

--------------------------------------------------------------------------

어렵지 않아 보이지만 실행 시간이 많이 소요되는 문제이다. 나누는 수가 a²이기 때문에 나머지를 확인하기 위해 검증하는 범위를 a²번까지 설정해야 했기 때문이다.

그리고, 나머지 함수의 특성을 살려서 적용해야지 문제에서 제시한 그대로 코딩했을 때에는 숫자가 기하급수적으로 커지면서 실행시간이 매우 많이 필요하게 되었다.

나머지 함수의 곱셈 특징((a*b)%c=(a%c)*(b%c))을 활용하여, 거듭제곱의 경우 분산해서 계산하도록 코드를 개선했다. 즉, a⁷=a*a²*a⁴, a⁹=a*a⁸과 같은 형태로 나누고, 각각에 나머지 함수를 적용해서 숫자가 최대한 커지지 않도록 만들었다.

그렇게 개선했어도 실행시간은 많이 필요했으며(100까지 7초, 200까지 58초, 300까지 173초, 400까지 360초, 500까지 628초, 600까지 942초, 700까지 1365초, 800까지 1777초, 900까지 2415초, 1000까지 3043초로 총 3시간 필요), 이 방식보다는 좀 더 빠른 형태의 수학에 기반한 해법이 있을 것 같다.

예를 들어 134468과 같이, 숫자를 왼쪽에서 오른쪽으로 읽을 때 각 자릿수가 이전 자릿수보다 작지 않으면 증가수라고 한다.

비슷하게, 예를 들어 66420과 같이 각 자릿수가 이전 자릿수보다 크지 않으면 감소수라고 한다.

예를 들어, 155349와 같이 증가하지도 감소하지도 않는 숫자를 bouncy number라고 한다.

명백하게, 100 미만으로는 bouncy number가 있을 수 없다. 1000 미만으로는 절반이 넘는 525개 숫자가 bouncy number이다. 실제로, bouncy number의 비중이 처음으로 50%가 되는 숫자는 538이다.

놀랍게도, bouncy number는 점차 많아져서 21780이 되면 bouncy number의 비중이 90%가 된다.

bouncy number가 정확히 99%가 되는 가장 작은 숫자를 찾으시오.

--------------------------------------------------------------------------

한 자리 숫자는 증가, 감소, bouncy가 있을 수 없으므로 10부터 시작해서 솟자를 계속 키워나가면서 증가수, 감소수, bouncy number를 판별하게 구성하면 된다.

구성할 때 한 가지 고려할 것은 이전 숫자와 값이 같으면 아직 증가수인지 감소수인지 판별을 유보해야 한다는 것이다. 처음에 이 부분을 잘못 생각하고 유보할 때 증가수, 감소수 플래그를 무조건 True로 값을 넣도록 프로그램을 만들었는데, 3자리에서는 유효하지만 4자리 숫자에서 오류를 만들게 되어 있어서 판별할 숫자를 50%만 제시했으면 이유를 찾지 못할뻔 했다. (값이 같을 때 이전에 증가수/감소수로 판별된 경우 이전 판별을 유지해야 되는데 잘 못 생각해서 계속 유보하게 만든 것이 문제였다)

조건문만 잘 구성하면, 반복문을 통해 까다롭지 않게 구할 수 있다.

−1000≤x,y≤1000인 좌표평면 위에 임의의 점을 3개 찍으면 삼각형을 만들 수 있다.

다음 두 삼각형을 생각해 보자:

A(−340,495), B(−153,−910), C(835,−947)

X(−175,41), Y(−421,−714), Z(574,−645)

삼각형 ABC에는 원점이 포함되지만, 삼각형 XYZ에는 원점이 포함되지 않는다.

27K 크기의 triangles.txt (우클릭하고 다른 이름으로 저장)에는 1,000개의 임의의 삼각형 좌표가 있다. 원점이 삼각형 안에 엤는 경우는 몇 개인가?

--------------------------------------------------------------------------

해결할 아이디어가 떠오르지 않아 찾아보니 고1 정도의 수학 지식을 필요로하는 문제였다. 벡터를 이용, 삼각형 면적 이용, 도형(삼각형)과 교차하는 점의 갯수, 무게중심좌표 등 해결하는 방법은 몇 가지가 있는데 개념은 알겠는데 실제 어떤 형태로 구현할 것인지는 쉽지 않았다.

이 중 무게중심좌표(Barycentric Coordinate System)를 이용한 해법으로 답을 구했다. 삼각형 세 꼭지점의 좌표를 (x1,y1), (x2, y2), (x3, y3)라 하고, 원점을(xp, yp)라 할 때, 다음과 같이 세 좌표를 계산해서 모두 0보다 크면 삼각형 내부에 있다고 한다.

alpha=((y2-y3)*(xp-x3)+(x3-x2)*(yp-y3)) / ((y2-y3)*(x1-x3)+(x3-x2)*(y1-y3))

beta=((y3-y1)*(xp-x3)+(x1-x3)*(yp-y3)) / ((y2-y3)*(x1-x3)+(x3-x2)*(y1-y3))

gamma=1.0-alpha-beta

왜 그렇게 되는지는 이해 못했지만 위 내용대로 구현하니 답을 구할 수 있었다.

그리고, 왜 이렇게 난이도가 올라갈까 싶었는데, 게임을 할 때 특정 좌표가 도형 내에 있는지 밖에 있는지 판단하는 방법으로 이 코드를 사용할 수 있다고 한다. 좌표가 보호막 내에 있는지 판단하거나, 게임 내의 비행체와 총알의 충돌을 판단하는 등에 사용할 것을 생각하면 이해가 필요한 것 같다.

프로젝트 오일러의 문제를 100번까지 모두 해결하는 것을 목표로 진행했는데, 몇 문제는 아이디어가 잘 떠오르지 않아 아직 해결하지 못했다. (특히 68번은 문제 자체를 이해할 수 없어 어떤 식으로 접근해야 할 지 오리무중이다) 이제는 난이도를 중심으로 해결되는 대로 포스팅할 예정이다.

100번대 이후 문제를 풀어보니, 난이도 5%도 문제대로 하면 코딩은 간단하지만 말도 안되는 수준으로 실행시간이 많이 필요하게 되어, 수학지식을 바탕으로 최적화하기를 요구하고 있는 등 적절한 방법으로 해결하는 것이 쉽지 않았다. 이제는 진짜 파이썬 공부인지 수학 공부인지 알 수 없어지는 상황이 되었지만, 그래도 최대한 해결해 볼 예정이다.